In this article, I'll share my analysis of the Longfellow Zero-Knowledge implementation of IETF's draft-google-cfrg-libzk-00 based on the paper titled "Anonymous credentials from ECDSA" by Matteo Frigo and Abhi Shelat.
People sometimes refer to this technology as the "Google-zk" especially following Google's PR about the adoption of this algorithm for privacy-preserving age verifications online based on government-issued digital IDs saved and presented using the Google Wallet.
Matteo Frigo, Google
The implementation has finally been named "longfellow-zk" by its authors, and I'll keep referring to it this way from now on. I'm grateful for the early access I was granted to the C++ code implementation, which is openly licensed as Apache/MIT throughout its code, and will soon be publicly available on Google's GitHub account.
Scientific summary
The Longfellow-zk algorithm is a diligent combination of the Ligero scheme (Lightweight Sublinear Arguments Without a Trusted Setup, 2022) and the Sum-Check protocol, which was first introduced in Algebraic Methods for Interactive Proof Systems (1992) and later became the building block for "Non-interactive zero-knowledge proofs" commonly referred to as zk-SNARKs.
The cryptographic methods are combined to create two zero-knowledge circuits that can operate in tandem to verify both ECDSA (P-256) signatures and SHA-256 hash identifiers found in a signed mdoc/mDL verifiable credentials.
Functional summary
This is rather important to understand.
The call graph of functions effectively illustrates the flow of this algorithm, which is relatively simple and therefore well-designed. There are just three main public calls defined in the lib/circuit/mdoc/mdoc_zk.h header I'll report here in simplified form:
- generate_circuit( int version )
- prover( circuit, mdoc, pk, transcript, attributes, time, zkspec)
- verifier( circuit, pk, transcript, attributes, time, proof, doctype, zkspec)
The Longfellow-zk public API currently operates on a limited, predefined array of attributes to prove and verify mdoc/mDL.
The circuit may be generated once and stored for reuse if all the presentation and verification flow is based on the same ZKSpec it was created for, including the number of attributes to be checked. In practice, this means that both holder and relying party apps should save pre-calculated circuits along with their creation settings, so that they can save a significant amount of computation time when it is possible to reuse them.
The mdoc is the signed document and is used only once by the prover function, while the verifier function will need to know its doctype.
The pk is the public key of the issuer, which has signed the MDOC.
The transcript is a signature computed by the user’s device on a transcript of the identity request. This second signature establishes device-bound soundness because the issuer verified that the holder's secret key is securely stored on the device at the time of issuance (POP).
Then there is time, which is a timestamp checked against the mdoc's issuance and expiration dates.
At last, attributes are an array of { id: "...", value: "..." } entries selected for disclosure; one must pay attention because a new circuit must be generated in case the number of disclosed attributes listed in the array ever changes.
The whole point is to process an MDOC through the prover and then, instead of presenting that, one should show the proof returned by this function.
The verifier will receive the proof and the doctype, along with other metadata, and verify that it is valid using the same issuer's public keys, which have been independently retrieved through a Public Key Infrastructure (PKI) proof.
So later on, while running the benchmarks, I'll be measuring the speed of the two calls, prover and verifier as well the quality of entropy (randomness) of the zero-knowledge proof exchanged, to establish how really privacy preserving this scheme is or, in other words, how it compares to random noise.
Compliance and standards
Longfellow-zk is designed to work with MDOC/mdl documents, enabling zero-knowledge presentation and the selective disclosure of credentials stored in mobile driver licenses used in the USA (with additional features to be added).
It also complies with the eIDAS 2.0 specification in Europe, which mandates support for the MDOC format in European Digital Identity wallets, issuers, and relying parties. It is also worth noting that the authors are already working on a circuit that can parse and verify JWT, but not SD-JWT, which would be a waste of time, and I wholeheartedly agree with them on this point.
The lab tests I've verified demonstrate support for the two following credential document formats:
- org.iso.18013.5.1.mDL (canonical as well as Sprind-Funke examples)
- com.google.wallet.idcard.1 (Google IDPass pilot for age verification)
Inside them, the verifications performed are at least three: P-256 ECDSA signatures, SHA-256 hashes, and expiry dates (formatted according to ISO 8601). More specifically:
- FIPS 180-4 secure hashes of 256 bits
- FIPS 186-4 ECDSA (NIST P-256)
The published source code indicates potential for improvement. For example, the use of C++ templating suggests that future support for additional elliptic curve signatures could be implemented. Notably, a comment references secp256k1, a cryptographic algorithm widely associated with Bitcoin. Also, some unused code is there to generate circuits that can verify SHA3 hashes (FIPS 202).
Benchmark
This benchmark is created using the Zenroom open-source VM version 5, which is written in C and has been verified to correctly pass tests found in the longfellow-zk code. Inside Zenroom, I've integrated an optimised build of longfellow-zk (libmdoc.a), which is written in C++ and therefore fully compatible.
Speed
I would like to start by saying that the benchmarks reported in the paper by Frigo and Shelat appear very reasonable and closely align with my own results.
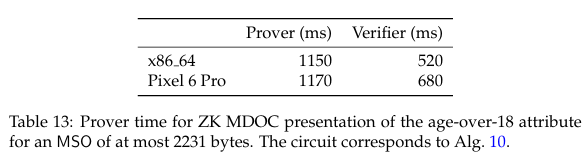
Using Zenroom's setup to run only the single claim tests, I get this average timing:
- Circuit generation: 6.76 (seconds)
- Prover: 795 (ms)
- Verifier: 466 (ms)
The reference implementation of longfellow-zk utilises OpenSSL cryptographic primitives, which leverage hardware acceleration for the two most commonly invoked functions: SHA256 and AES-ECB. However, this choice complicates the implementation by introducing another significant dependency, which raises both licensing and portability issues.
I have therefore contributed build-time switches and small C implementations of these primitives to bypass OpenSSL, utilising only public-domain code without explicit hardware acceleration. The benchmark results in the same conditions as the previous tests are then:
- Prover: 816 (ms)
- Verifier: 492 (ms)
Half a second for a single credential verification.
Considering these benchmarks, I believe it is wise to remove the OpenSSL dependency, which is only needed for SHA256, AES-ECB, and a random source.
The difference in speed brought by OpenSSL may be bigger on other architectures like ARM, however I believe the small speed gain does not justify the increase in implementation and deployement complexity, especially considering the portability aspect: it is rather trivial then to compile longfellow-zk with my patches for WASM targets, to make it run in-browser, with the small addition of a piece of SIMD128 assembler routine I've also contributed to the project.
One last caveat for anyone out there willing to compare longfellow-zk to other zero-knowledge proof algorithms: this is a benchmark of the whole MDOC ZK prover and verifier, not just of a single string or key: the ZK circuit executes an MDOC/mdl parser, a P256 signature verification and a SHA256 hash computation. This is significantly more than the typical ZK primitive, as seen, for instance, in my BBS benchmark here. Comparing Longfellow-ZK and BBS at this stage is misleading unless someone develops a complete ZK circuit in BBS that performs the same function as Longfellow-ZK.
Size
The two main artefacts to measure here are the circuit and the proof, and so far, I've been testing them only for single claim presentations.
The circuit is aptly compressed using ZSTD by the longfellow-zk library itself. When reading the code, I've been immediately sceptical about adding the dependency of a compression library inside the codebase. Still, the reason for this choice became clear at the first measurement.
The uncompressed size of a circuit ranges from 85 to 100 MB; it increases when generated to parse more than one attribute. When compressed, it reduces to a base64-encoded binary blob of 315 KB. That is an impressive compression ratio! Hinting that there must be a lot of repetition in the raw circuit binary rendering.
The proof size varies slightly across single-claim tests, with an average of 325 KB.
A proof is between 325 kilobytes for a single attribute.
The results of this benchmark clearly show that proofs are too big to be transferred via near-field communication channels (NFC) or QR codes. However, their zero-knowledge nature enables a variety of approaches to the problem.
Privacy
This measurement provides insights into the privacy level of the zero-knowledge proofs produced by longfellow-zk: the binary material exchanged "in public" or at least between holder and verifier (also called relying party).
This is a type of laboratory measurement that does not cover all possible configurations. It is of interest primarily because it allows us to view longfellow-zk through the perspective of an eavesdropper intercepting data and searching for identifiable fingerprints.
The test performed consists of measuring the Hamming distance between different presented proofs of the same credential. I do this many times, and show the frequencies of repetition of measured distances.
Then I repeat the same process with random values to obtain a graph that compares the most frequent distances between random values and between Longfellow-ZK proofs. I compare it to two types of random feeds:
- PRNG is the default pseudo-random generator in Zenroom, using a 64-byte seed sequence provided by the operating system and hashed with the timestamp at the time of execution.
- RORG is again the PRNG in Zenroom, initialised with a seed that is retrieved online from Random.org at the time of execution.
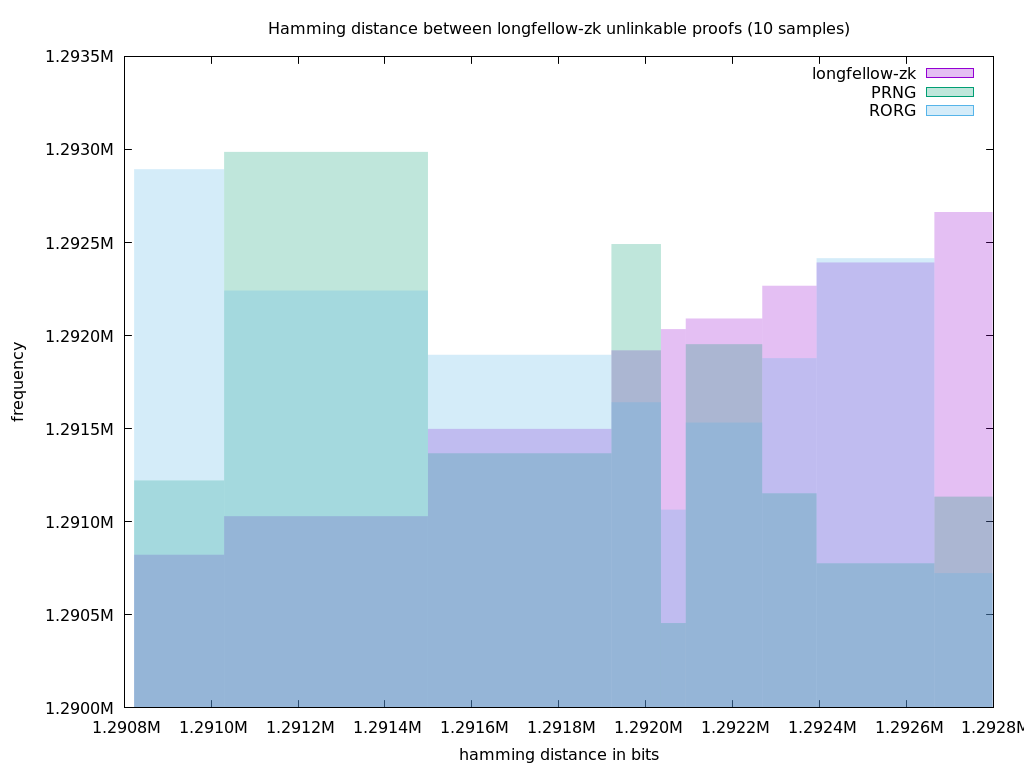
In this first run, I'm using only 10 samples from each source, comparing the frequency of hamming distance between adjacent samples on each stream.
Now with 10000 samples:
What we see in this analysis are overlapping graphs of the most frequent values. The frequency is centred around 1288000 bits, which is a safe value for the 322KiB long sequences I have been analysing: comparing a total of 2576000 bits each time, it is precisely half of the total.
It appears that Longfellow-ZK proofs yield slightly lower Hamming distance values, but I believe this is not particularly important.
Additionally, by employing the classic Shannon measurement for entropy (a built-in octet method in Zenroom), we obtain values ranging from 0.97 to 0.98, which are consistent with those for generated cryptographic random data.
Security considerations
This section is still incomplete, and I plan to bring it to the attention of the W3C Security Interest group I'm co-chairing to get a better assessment, which will most likely occur after the Global Digital Collaboration conference in Geneva where I will hold a small speech about all this.
Get in touch if you like to meet or attend in Geneva!
Meanwhile, I will list here four notable security aspects I see in longfellow-zk.
It may be considered post-quantum secure
Also, according to explicit claims made by Matteo Frigo, which I'll take time to debunk. The principle of post-quantum safety relies on the use of SHA-256 as the random oracle primitive adopted for soundness and zero-knowledge.
It is compatible with TEE / SE implementations
Hardware enclaves are designed to conceal private keys, storing them in hardware-protected memory that prevents users from knowing their own secret key, copying it, or sharing it on other devices. This principle is supported by the adoption of the P256 (secp256r1) EC curve and ECDSA signature, which has been historically supported on these chips and is performed in hardware on many mobile phones.
The ZK circuit binary is a new attack surface
A circuit is somewhat akin to firmware for the computation operated by Longfellow-ZK. We will not see many circuits around, and they will all be "blessed" and authenticated by those of us who understand their complexity, for operating as intended. A new attack surface is opened by the hypothesis of malicious circuits being injected into operations, which may entirely counterfeit their results, i.e., producing linkable proofs or faking verifications.
Random number generator attacks
At last, a small unverified security concern I have is that the random number used to generate zero-knowledge proofs is not processed by a PRNG, but it is data returned by any random source and used as-is. This aspect should be more carefully verified, as I am concerned that it makes the algorithm vulnerable to random number generator attacks.
Integration
While at the GDC25 in Geneva we showcased a native Android app integrating longfellow-zk, the code: https://github.com/dyne/Zenroom-Android-app
To try it out live, runing a zk-proof generation of the Sprind-Funke example MDOC for age verification, the APK can be downloaded using the QR below:
Contact us if you are interested in having the .AAR lib to integrate it in your app.
Conclusion
The buzz around longfellow-zk seems to be based on true assumptions: it is a privacy-preserving algorithm that has a competitive edge in terms of interoperability with legacy infrastructure. While it does not compromise on speed, the only negligible issue is the size of proofs, which definitely does not fit into NFC or RFID channels.
Nowadays, many public institutions have faith in Trusted Execution Environments (TEE) provided by consortia of hardware and operating systems. In my article on the Seven Sins of EUDI, I explain why this is a foolish posture. Yet, especially in the public sector, technical specifications often insist on relying on hardware for security. Longfellow-ZK represents a unique opportunity to grant citizens the privacy they deserve, while adhering to existing standards and hardware chips already present in mobile devices.
On the other hand, given the low ambition of the eIDAS 2.0 specification regarding citizens' privacy (among other issues), I believe that longfellow-zk represents an important tool for us, as unheard citizens and scientists, to highlight the negligence of the European Commission in the event that this technology isn't adopted. We can make it production-ready within a year through community adoption, as Google appears to be doing in the USA already.
Longfellow-zk leaves no more excuses for not adopting privacy-preserving tech for digital wallets.
I'll conclude with two more points that aren't mentioned in the Longfellow-Zk paper or its RFC draft, but I was fortunate enough to understand through my interactions with brilliant scientists, such as Frigo and Shelat.
Revocation
We believe that the authors have in mind a revocation system for longfellow-zk credentials, and it will be privacy-preserving in virtue of a "revocation range" mechanism. In brief, credentials are revoked using signed ranges and zero-knowledge proofs (ZKPs).
- Issuer signs ranges
Instead of signing each credential, the issuer signs blocks (i.e., 1-100, 101-200). - Holder fetches their range
A holder downloads the signed block containing their credential. - Holder proves inclusion (or exclusion) via ZKP
Without revealing the exact credentials, they prove:- Their credential is in a valid, issuer-signed range (or not, if revoked).
- The range’s signature is authentic.
The key tradeoffs of this approach are: efficiency (fewer signatures than per-credential revocation), privacy (ZKPs hide which credential is being verified), and freshness (revocation requires range updates). This will work if ZKPs are sound and ranges are managed carefully, but real-world use will demand scrutiny.
Verification without the issuer's public keys
This positively surprised me: authors have mentioned that it is already possible, with a few tweaks, to run proof verifications without the issuer's public key. They are keen to develop this feature as a means of privacy protection, because issuers can always use different public keys to distinguish and trace holders. Although there is no documentation about this yet, I tend to trust that this project will bring groundbreaking innovation to the world of identity, and this would just be the cherry on top.
Tl;dr
Stay in touch
If you want to implement the Longfellow-ZK Signature Scheme, you are free to use Zenroom; no need to know coding or complex math for that. Start from our developer documentation and try some examples on our free online IDE.
If you need help integrating Longfellow-ZK into your product, do not hesitate to contact us at Forkbomb Company. We are keen to hear from you!
For professional support email info@forkbomb.eu
Get professional support
🎓 About the author
This article is written by:
