In this article, I'll analyze the speed of execution, size, and entropy of zero-knowledge proofs for the BBS Signature Scheme, as described by the version 06 draft submitted to the Internet Research Task Force.

This benchmark is based on the Zenroom open-source implementation of BBS which is written in C and is verified to correctly match vectors found in appendix J.9.1 of the BBS draft version 06. The source code written to perform these benchmarks is found in the test/benchmark/bbs folder shipped inside the Zenroom source code.

Speed
Compared to other zero-knowledge proof algorithms available in Zenroom, BBS clearly shows to be the fastest implementation, in some cases even by one order of magnitude.
Keypair generation (public key computation from random material) takes between 0.0025 and 0.003 seconds, in other words, that is between two and a half and three milliseconds.
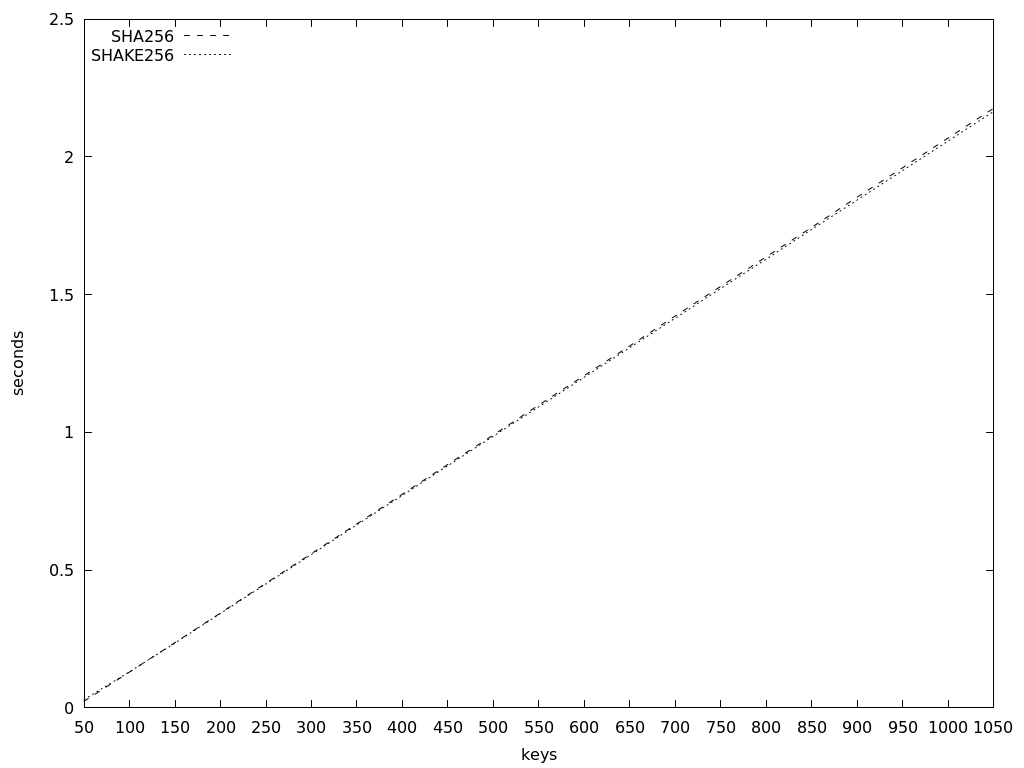
When operated on a growing number of keypairs, the growth is linear and there is no substantial difference between the SHA256 and SHAKE256 implementations. In all following speed tests, I noted the performance of these two implementations stays the same, so I'll limit benchmarks to use SHAKE256 for simplicity.
Issuance takes between 0.006 and 0.0075 seconds to have a single credential signed, in other words between six and seven and a half milliseconds. Clear-text verification takes slightly less.
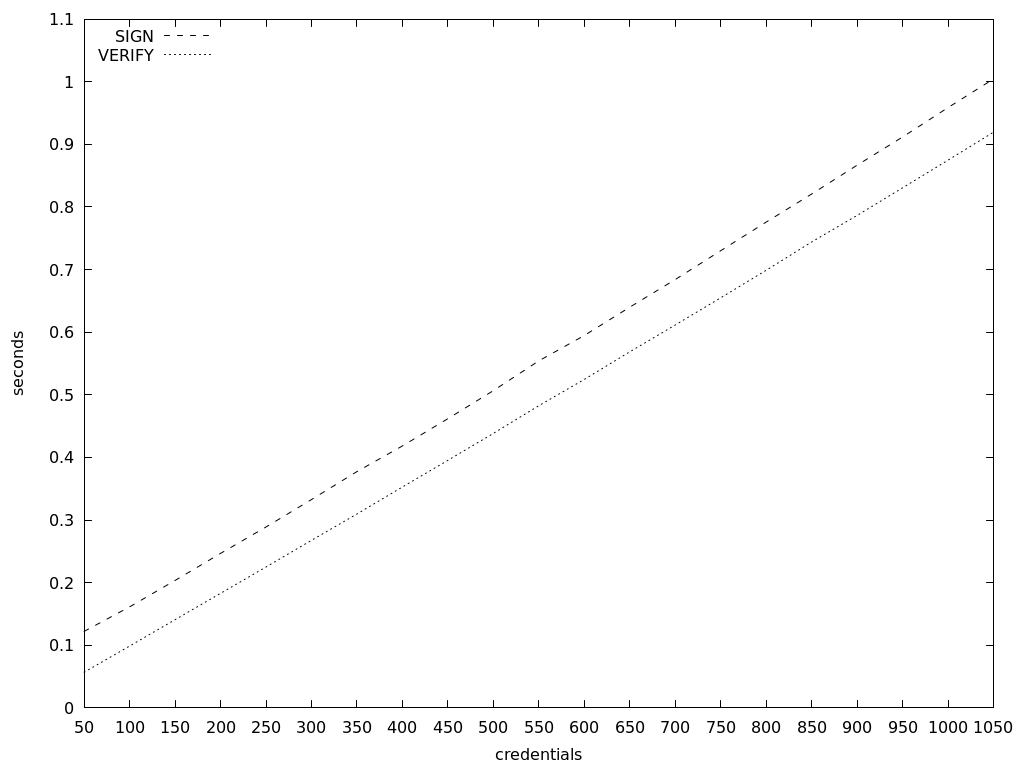
Presentation of zero-knowledge proofs takes between 0.0084 and 0.0095 seconds to disclose a single proof, which is almost one centisecond.
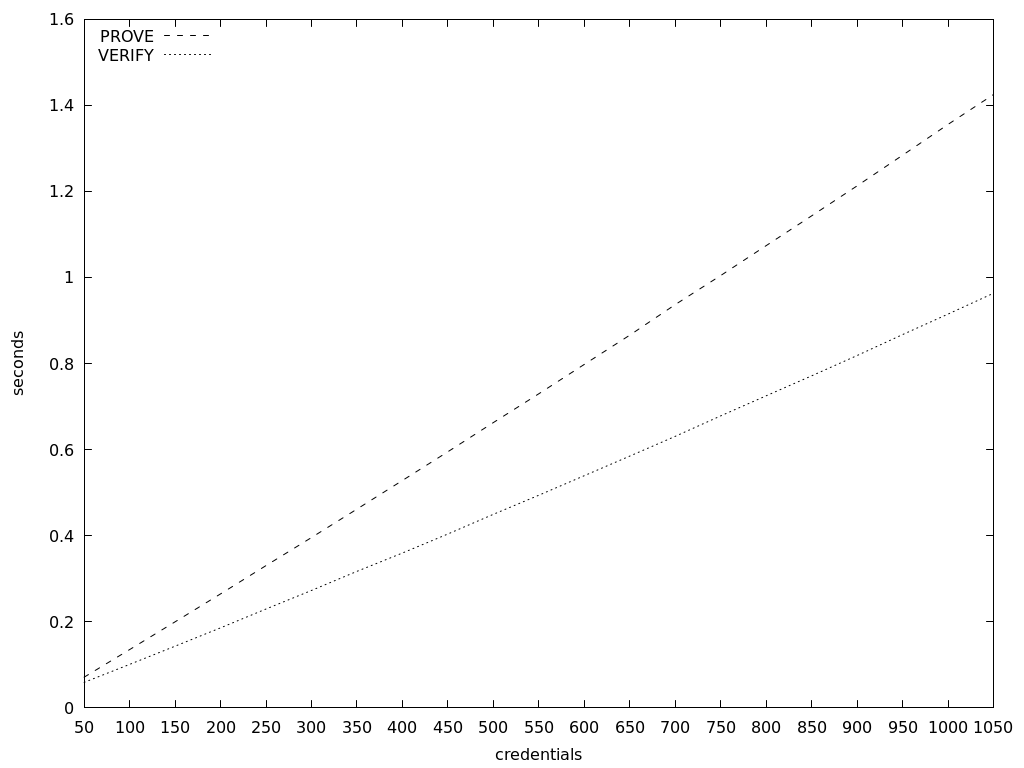
Verification of zero-knowledge proofs takes approximately 0.019 seconds, which is almost 2 centiseconds to verify a single proof.
However. when performed on a growing number of credentials, it becomes evident that BBS verification is faster than the presentation. The graph's bottom starts from fifty credentials and shows linear growth.
Almost a second and a half for a thousand credential verifications.
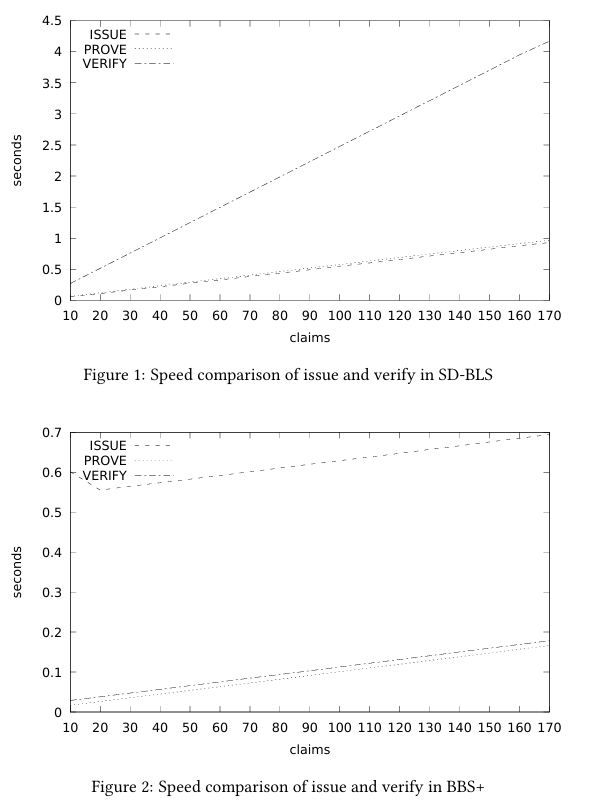
It is worth mentioning that BBS is one order of magnitude faster than Boneh-Lynn-Shacham (BLS) signatures operated on the same BLS12-381 curve and under the same conditions (Zenroom implementation and benchmark hardware), showing BBS is well optimized. We compared these two signatures in the benchmarks section of our recent SD-BLS paper, also available as open-access on Arxiv.
Size
Using BBS seems to be also good for saving on size: both the issuer public keys and the presentation proofs are generally smaller than other competitors.
I measure that:
- Public keys are 96 bytes long
- Issued signatures are 80 bytes long
- Zero-knowledge proofs of a single credential are 272 bytes long
Based on this information, you can calculate the additional storage requirements BBS will introduce to your database or decentralized ID storage.
For instance to have a hundred issuers listed in your DID domain will add less than 10KB space, which makes it easy to maintain a static list of issuance authorities inside any application.
Yet we must take into account that BBS zero-knowledge proofs can be created for multiple credentials and a selected amount of disclosed credentials among them. After a few tests, it becomes clear that the size of proof is affected by the total amount of credentials, and not by the amount of disclosed ones, nor by the size of the credential string.
It is easy to measure the growth in the size of the proof since it is just related to the amount of total signed credentials:
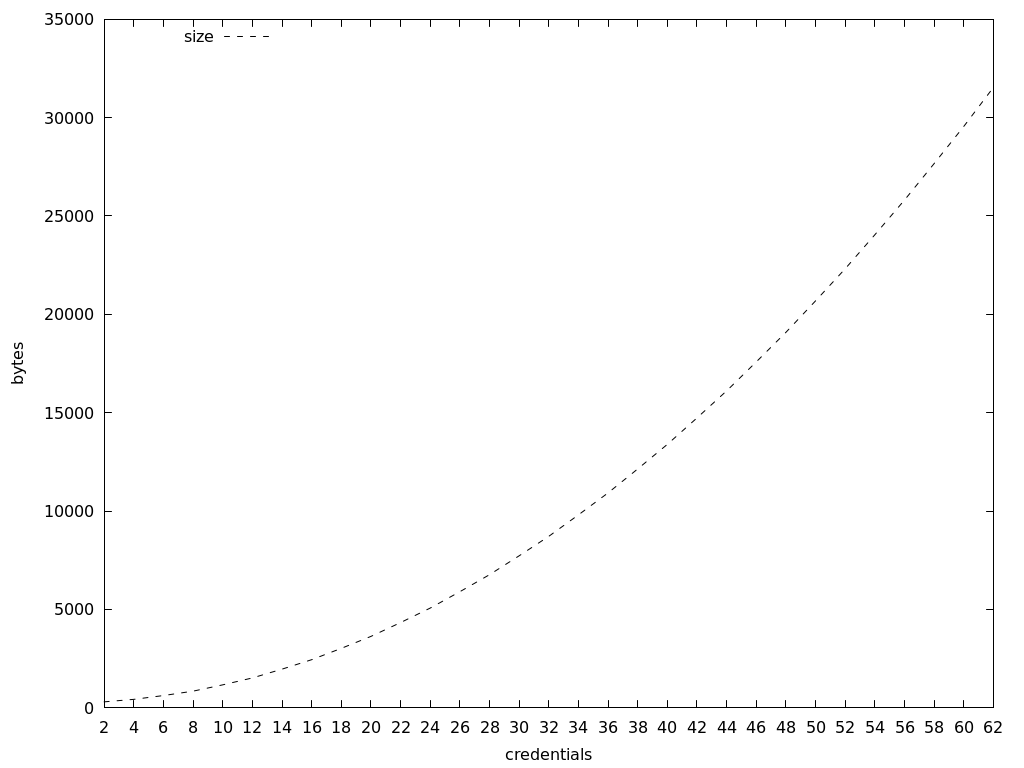
The growth is not linear, but logarithmic.
For instance, my lab test shows these exact numbers:
| Credentials | Bytes |
|---|---|
| 35 | 4496 |
| 50 | 8688 |
| 100 | 33072 |
| 200 | 129872 |
A typical mobile wallet application will hold a hundred credentials in less than 10KB but will be able to use a QR code to present proof for them only if the total amount of signed credentials is 35, considering its core material and some metadata will require approximately 300 bytes, leaving no space for a picture.
Privacy
This measurement provides insights into the privacy level of BBS zero-knowledge proofs. However, it represents a type of laboratory measurement that does not cover all possible configurations. It is of interest primarily because it allows us to view BBS through the perspective of an eavesdropper intercepting data and searching for identifiable fingerprints.
The test performed consists of measuring the Hamming distance between different presented proofs of the same credential. I do this many times and show the frequencies of repetition of distances.
Then I do the same with random values to obtain a graph that compares what are the most frequent distances between random values and between BBS proofs. Since random can differ depending on the PRNG implementation and also on the seed, I added three types of random feeds:
- PRNG is the default pseudo-random generator in Zenroom, using as seed a sequence of 64 bytes provided by the operating system and hashed with the timestamp at the time of execution.
- RORG is again the PRNG in Zenroom, but initialized with a seed that is retrieved online from Random.org at the time of execution.
- OSSL is made of random values provided by the OpenSSL library installed.
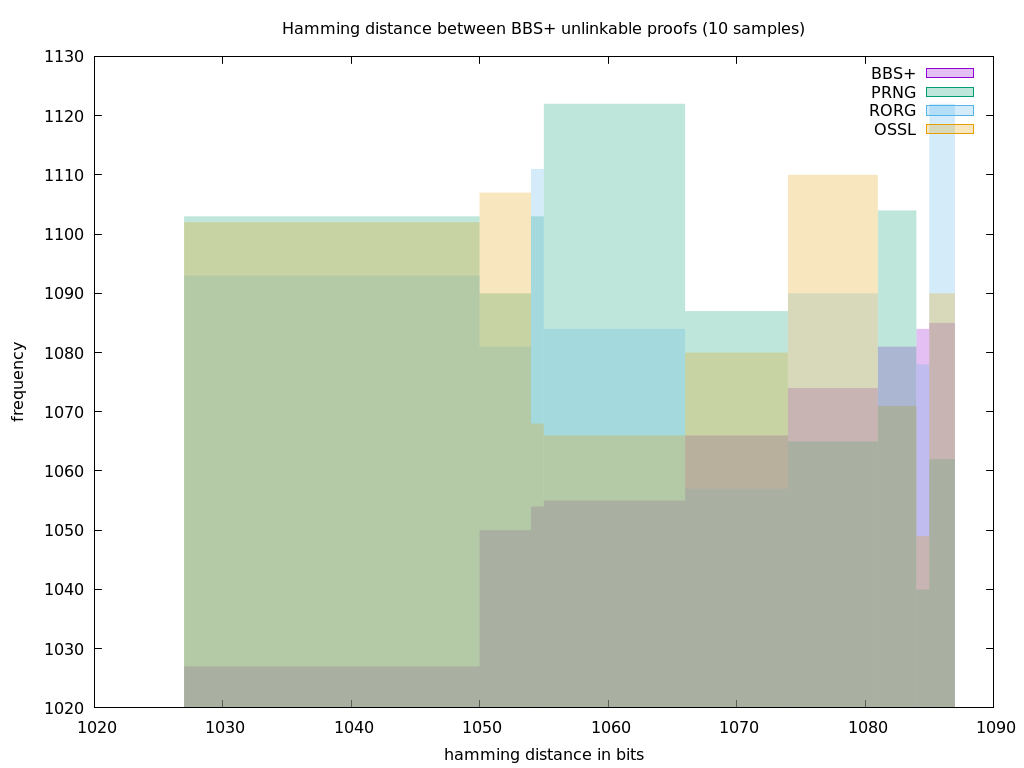
In this first run, I'm using only ten samples from each source, comparing the frequency of hamming distance between adjacent samples on each stream.
Now with a hundred samples:
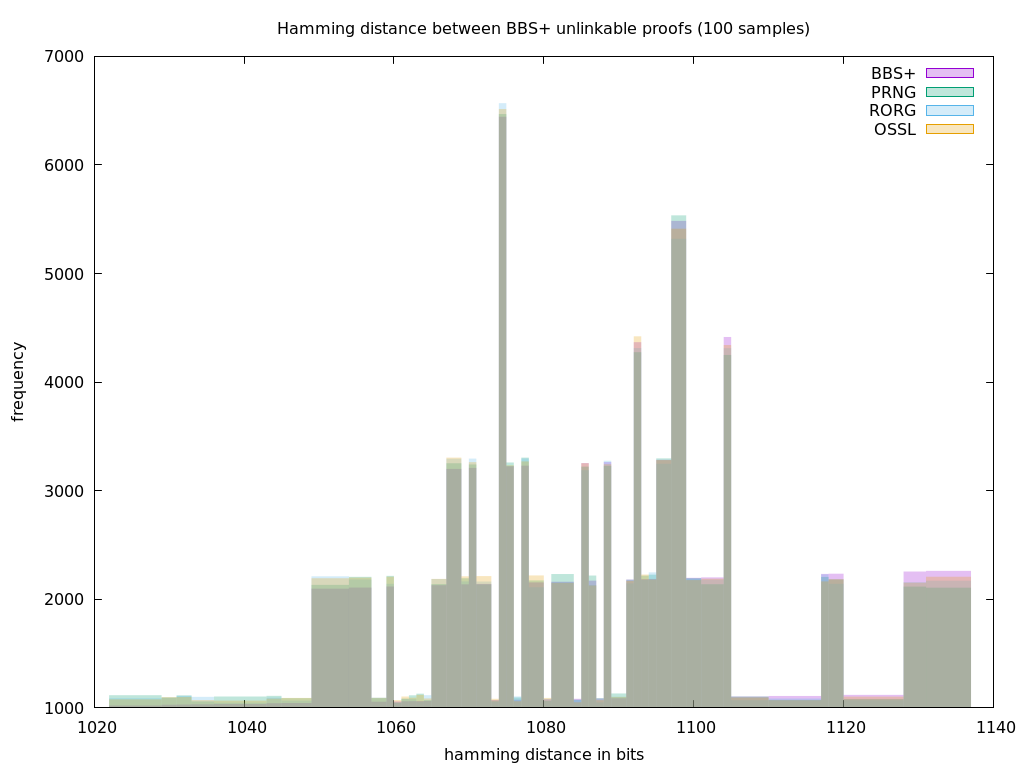
And up to a thousand samples:
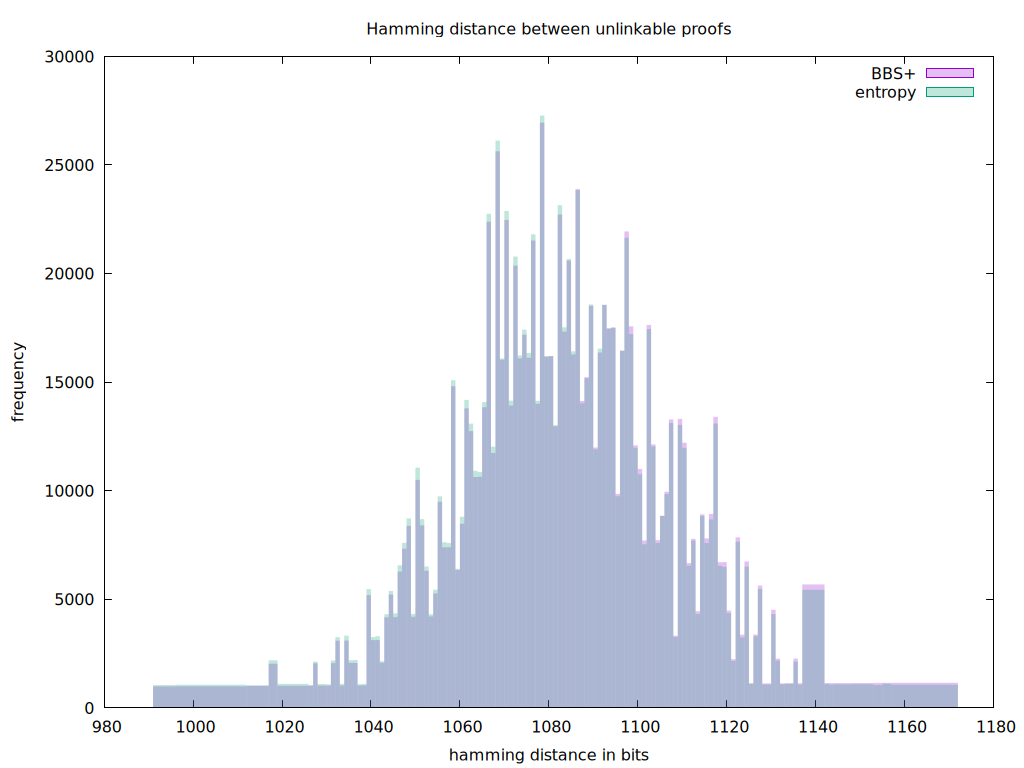
What we get after this analysis are overlapping graphs of the most frequent values. The frequency is centered around 1080 bits which is pretty normal for the 272-byte long sequences we are analyzing, comparing a total of 2176 bits each time. It even looks like BBS zk proofs yield slightly higher hamming distance values, which is a good sign.
Also adopting the classic Shannon measurement for entropy (a built-in octet method in Zenroom), we obtain values between 0.97 and 0.98 which are the same for generated cryptographic random data.
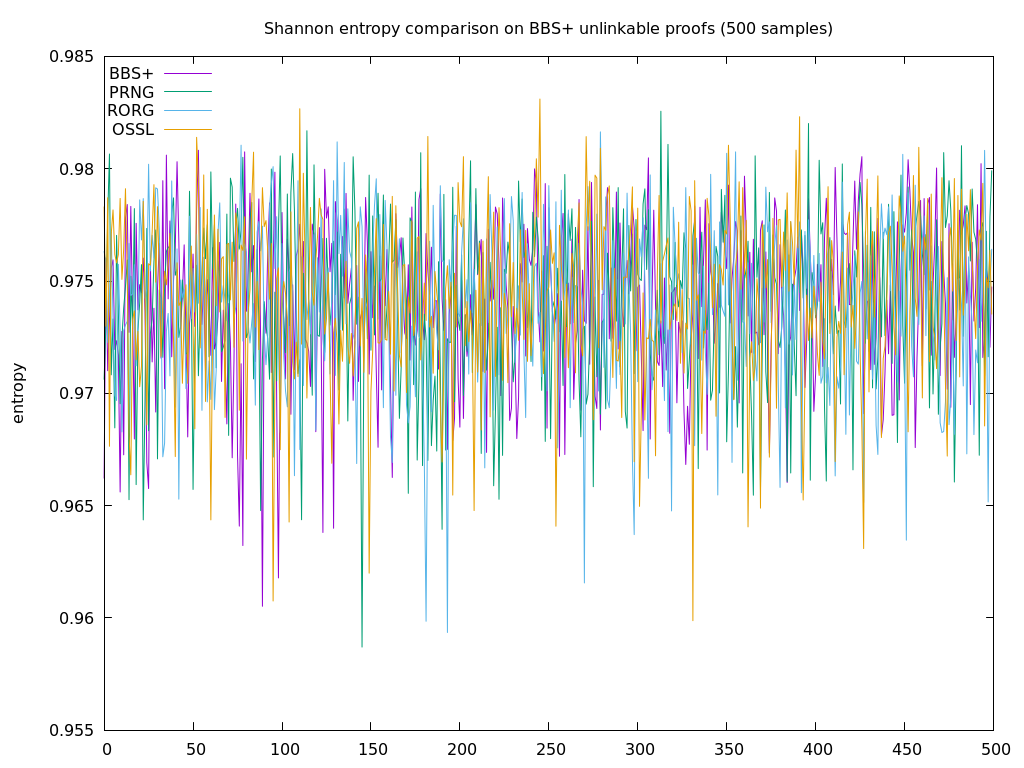
More precisely measuring the "entropy" of 500 proofs with a floating value between zero and one I could observe that:
- The BBS ZK proof average is 0.974081
- Zenroom's PRNG average is 0.9742654
- Zenroom's PRNG with a Random.org seed average to 0.9738644
- OpenSSL's random averages to 0.9738644
You are welcome to repeat this benchmark on your systems: I've done my best to make the hamming.sh script portable, it will require Zenroom and Gnuplot installed, along with source files common.lua and hamming.lua in the same folder.
Security considerations
While running these benchmarks I've noticed there is some fragility in the BBS algorithm which can be exploited by malformed proof and disclosure indexes: the array of integer numbers passed as argument to proof and disclosure functions, used to indicate which credentials are to be proven and disclosed.
I don't think this is unique to our implementation, in any case, this is a caveat for anyone else implementing a BBS system that goes into production.
An application implementing a BBS wallet should always take care that:
- Indexes do not contain duplicate values
- Values contained in indexes do not exceed the total amount of credentials
- Zero as a value is never contained in an index
Since indexes will likely be a parameter exposed to user interaction, for instance selecting through checkboxes which credentials to prove and disclose, then the BBS implementation should take care to validate carefully this input.
Conclusion
The buzz around BBS seems to be based on true assumptions: it is a privacy-preserving algorithm that has a competitive edge in terms of speed and size when compared to other zero-knowledge-proof implementations.
The data integrity assessment on BBS interoperability is in the works and shows how multiple implementations can talk to each other. And more generally more standardization efforts are going towards its way.
What may be holding some institutions back from BBS adoption is their faith in Trusted Execution Environments (TEE) provided by clans of hardware and operating systems manufacturers.
Integrated hardware TEEs are too outdated to support the sort of EC pairing mathematic operations needed by BBS, ruling it out. I don't hide my skepticism about TEE maxis here, because they ignore many security attacks in the wild and because their trust architecture is a weak pyramid lacking any resilience.
As it's made evident by the failing process of the EUDI ARF, the price to pay for TEE fanaticism may be as high as the privacy of European citizens.
Stay in touch
If you want to implement the BBS Signature Scheme, you are free to use Zenroom, no need to know coding or complex math for that. Start from our developer documentation and try some examples on our free online IDE.
And if you need help to integrate it into your product, do not hesitate to contact us at the Forkbomb company, we are keen to hear from you!
For professional support mail info@forkbomb.eu

Get professional support
🎓 About the author
This article is written by:







